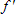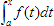Grade(s): 10-12
Length: Two semesters
Prerequisites: Algebra B
| Numbers and Operations
|
- Use models, explanations (verbal & written), number lines, real-life situations, descriptions and illustrations to demonstrate the effects of arithmetic operations on real numbers
- Use models, explanations, number lines, real-life situations to describe and illustrate the use of inverse operations (squaring/square root)
- Apply the rules of order of operations to real numbers and variables
- Use the distributive property with variables.
- Judge whether a strategy will result in an answer greater or less than the exact answer
- Add, subtract, multiply, and divide rational numbers including integers with whole number exponents
- Determine rate by using ratio and proportion
- Explain why one strategy is more appropriate than another and determine why the estimated result is greater or less than the exact number
|
| Measurement
|
- Convert square and cubic units within the same system and between English or metric systems (using a conversion factor)
- Apply indirect methods, such as the Pythagorean Theorem to find missing dimensions in real-world applications
|
| Statistics & Probability
|
- Design, collect, organize, display, and explain the classification of data in real-world problems using information from tables or graphs that display two sets of data (or with technology)
- Determine and compare the experimental and theoretical probability of independent or dependent events
- Make predictions about the probability of independent and dependent events and use the information to solve problems
- Design, conduct, analyze, and communicate the results of a probability experiment
|
| Functions & Relationships
|
- Generalize relationships (linear, quadratic, absolute value) using a table of ordered pairs, a graph, or an equation
- Use a calculator as a tool when describing, extending, representing, or graphing patterns or equations
- Solve literal equations or formulas for a given variable
- Describe in words how a change in one variable in a formula affects the remaining variables
|
| Geometry
|
- Use a coordinate plane to solve problems involving congruent or similar shapes
- Draw and describe the results of applying transformations (translations, rotations, reflections, or dilations) to figures on a coordinate plane
- Determine the perimeter and area of 2-dimensional figures
- Determine the volume and surface area of prisms, cylinders, cones, pyramids, spheres, and compound solids
- Graph or identify (using equations and formulas) the slope of line segments on a coordinate plane
- Identify, analyze, compare, and use properties of plane figures:
- Supplementary, complementary and vertical angles
- Angles created by parallel lines with a transversal
- Sum of interior and exterior angles of a polygon
- Central angles, chords, inscribed angles and arcs of a circle
- Use transformations to show congruence or similarity of figures on a coordinate plane
- Graph a line segment on a coordinate grid and identify its length and midpoint by using formulas
- Draw, measure, and construct geometric models of plane figures (containing parallel and/or perpendicular lines, angles, perpendicular bisectors, congruent angles, and regular polygons)
|
| Problem Solving
|
- Select, modify, and apply a variety of problem-solving strategies and verify the results
- Apply multi-step integrated mathematical problem-solving strategies
- Evaluate, interpret, and justify solutions to problems by using an alternative strategy
- Verify an answer by using an alternative strategy
- Follow and evaluate an argument, judge its validity using inductive or deductive reasoning and logic; or make and test conjectures
- Use methods of informal proof including direct, indirect, and counterexamples to validate conjectures
- Use mathematics in real-world contexts such as science, humanities, among peers, community, national issues, global issues, and careers
- Represent mathematical problems numerically, graphically, and algebraically, communicate math ideas in writing; and use appropriate vocabulary, symbols, or technology to explain, justify, and defend strategies and solutions
|
Grade(s): 9-12
Length: Two semesters
Prerequisites: Algebra I
| Numbers and Operations
|
- Use models, explanations (verbal & written), number lines, real-life situations, descriptions and illustrations to demonstrate the effects of arithmetic operations on real numbers
- Use models, explanations, number lines, real-life situations to describe and illustrate the use of inverse operations (squaring/square root, cubing/cube root)
- Apply order of operations rules to real numbers and variables
- Use the distributive property with variables.
- Simplify expressions with positive exponents
- Express square roots in simplest radical form
- Judge whether the strategy will result in an answer greater or less than the exact answer
- Add, subtract, multiply, and divide real numbers including integers with whole number exponents
- Determine rate by using ratio and proportion
- Explain why one strategy is more appropriate than another and determine why the estimated result is greater or less than the exact number
|
| Measurement
|
- Apply indirect methods, such as the Pythagorean Theorem to find missing dimensions in real-world applications
- Convert square and cubic units within the same system and between English or metric systems (using a conversion factor)
- Apply right triangle trigonometry (sine, cosine, and tangent) to find missing dimensions in real-world applications
|
| Statistics & Probability
|
- Design, collect, organize, display, and explain the classification of data in real-world problems using information from tables or graphs that display two sets of data (or with technology)
- Determine and compare the experimental and theoretical probability of independent or dependent events
- Make predictions about the probability of independent and dependent events and use the information to solve problems
- Design, conduct, analyze, and communicate the results of a probability experiment
|
| Functions & Relationships
|
- Generalize relationships (linear, quadratic, absolute value) using a table of ordered pairs, a graph, or an equation
- Use a calculator as a tool when describing, extending, representing, or graphing patterns or equations
- Describe in words how a change in one variable in a formula affects the remaining variables
- Describe in words how a change in one variable or constant in an equation affects the outcome of the equation
- Model (graphically and algebraically) and solve situations (including real-world applications) using systems of linear equations or inequalities
- Solve or identify solutions to literal equations or formulas for a given variable involving multi-steps
|
| Geometry
|
- Use a coordinate plane to solve problems involving congruent or similar shapes
- Draw and describe the results of applying transformations (translations, rotations, reflections, or dilations) to figures on a coordinate plane
- Determine the volume or surface area or prisms, cylinders, cones, pyramids, spheres, and compound solids
- Graph or identify (using equations or formulas to determine the slope of line segments) on a coordinate plane
- Draw, measure, or construct geometric models or plane figures (containing parallel and/or perpendicular lines)
- Identify, analyze, compare, or use properties of plane figures:
- Supplementary, complementary and vertical angles
- Angles created by parallel lines with a transversal
- Sum of interior and exterior angles of a polygon
- Central angles, chords, inscribed angles and arcs of a circle
- Use transformations to show congruence or similarity of figures on a coordinate plane
- Graph a line segment on a coordinate grid and/or identify its length or midpoint by using formulas
- Draw, measure, or construct geometric models of plane figures (containing parallel and/or perpendicular lines, angles, perpendicular bisectors, congruent angles, regular polygons)
- Graph a system of equations on a coordinate grid, identify a solution, or determine their relationship (intersecting, parallel, perpendicular)
|
| Problem Solving
|
- Select, modify, and apply a variety of problem-solving strategies and verify the results
- Apply multi-step integrated mathematical problem-solving strategies
- Evaluate, interpret, and justify solutions to problems by using an alternative strategy
- Verify the answer by using an alternative strategy
- Follow and evaluate an argument, judge its validity using inductive or deductive reasoning and logic; or make and test conjectures
- Use methods of formal proof including direct, indirect, and counterexamples to validate conjectures
- Use real-world contexts such as science, humanities, peers, community, careers, national issues, and global issues
- Represent mathematical problems numerically, graphically, and/or symbolically, communicating math ideas in writing; and using appropriate vocabulary, symbols, or technology to explain, justify, and defend strategies and solutions
|
Grade(s): 9-12
Length: Two semesters
Prerequisites: Geometry (or equivalent)
| Numbers and Operations
|
- Write equivalent representations of the same exponential expression
- Identify the subsets of complex numbers (natural, whole, integers, rational, irrational, real, and imaginary)
- Simplify expressions with positive and negative exponents
- Express radical expressions in simplest radical form
- Describe and illustrate the effects of arithmetic operations on complex numbers
- Describe and illustrate the use of inverse operations (cubing/cube root)
- Identify and apply commutative, identity, associative, inverse, and distributive properties to complex numbers and variables
- Identify and write the prime factorization of a variable expression using exponents
- Explain why one strategy is more appropriate than another and determine why the estimated result is greater or less than the exact answer
- Apply basic operations with complex numbers using powers
|
| Measurement
|
- Convert square and cubic units within the same system and English or metric systems (using a conversion factor)
|
| Statistics & Probability
|
- Design, collect, organize, display, and explain the classification of data in real-world problems, using information from tables and graphs that display two or more sets of data (or with technology)
- Use information from a display to solve a problem or analyze the validity of statistical conclusions
- Use a line of best fit to describe trends and make predictions about data
- Explain in words or identify the difference between experimental and theoretical probability of independent or dependent events
- Analyze data to make predictions about the probability of independent or dependent events as a basis for solving real-world problems
- Design, conduct, analyze, and communicate the results of a multi-stage probability experiment
- Identify and apply combinations and permutations
|
| Functions & Relationships
|
- Describe and extend patterns represented in tables, graphs, and in real-world situations using these relations:
polynomial, absolute value, exponential, logarithmic, rational, radical, inverse functions, arithmetic and geometric sequences and series up to the nth term
- Describe in words how a change in one variable or constant in an equation affects the outcome of the equation
- Use a calculator as a tool when describing, extending, representing, or graphing patterns, polynomial, rational, radical, exponential and logarithmic functions
- Represent linear, quadratic and absolute value inequalities using a graph
- Model (graphically and algebraically including matrices) and solve situations (including real-world applications) using systems of linear equations or inequalities
- Select and use the quadratic formula, completing the square or factoring to solve problems
- Solve and identify solutions to literal equations or formulas for a given variable involving multi-steps
- Simplify polynomial expressions
- Apply algebraic properties to solve equations (polynomial, rational, radical, exponential, logarithmic)
|
| Geometry
|
- Use transformations applied to functions to show congruence or similarity of figures on a coordinate plane
- Graph a system of equations or inequalities (linear programming) on a coordinate grid, identify a solution and determine their relationship (intersecting, parallel, perpendicular)
|
| Problem Solving
|
- Follow and evaluate an argument, judge its validity using inductive or deductive reasoning and logic; and make and test conjectures
- Apply multi-step, integrated mathematical problem-solving strategies
- Verify an answer by using an alternative strategy
- Represent mathematical problems numerically, graphically, and algebraically, communicate math ideas in writing; and use appropriate vocabulary, symbols, or technology to explain, justify, and defend strategies and solutions
- Use methods of proof including direct, indirect, and counterexamples to validate conjectures
- Apply mathematics to real-world contexts such as global issues and careers
|
Grade(s): 8-10
Length: Two Semesters
Prerequisites: Teacher recommendation
| Numbers and Operations
|
- Convert between a rational number in scientific notation and standard form
- Equate different equivalent representations of the same exponential expression
- Use models, explanations, number lines. real-life situations to describe and illustrate the effects of arithmetic operations on real numbers
- Use models, explanations, number lines, real-life situations to describe and illustrate the use of inverse operations (squaring/square root, cubing/cube root)
- Apply the rules for order of operations to real numbers and variables
- Identify the subsets of real numbers (natural, whole, integers, rational, irrational)
- Simplify expressions with positive and negative exponents
- Express square roots in simplest radical form
- Identify and apply commutative, identity, associative, inverse, and distributive properties to real numbers and variables
- Identify and write the prime factorization of a variable expression using exponents
- Judge whether the strategy will result in an answer greater or less than the exact answer
- Add, subtract, multiply, and divide rational numbers, including integers with whole number exponents
- Determine rate by using ratio and proportion
- Multiply or divide numbers in scientific notation
- Apply basic operations with real numbers using powers
- Solve problems involving percent increase or decrease
|
| Measurement
|
- Estimate and convert measurements within the English and metric systems in real-world applications, given a conversion factor
- Apply indirect methods, such as the Pythagorean Theorem to find missing dimensions in real-world applications
|
| Statistics & Probability
|
- Design, collect, organize, display, and explain the classification of data in real-world problems, using information from tables and graphs that display two or more sets of data( or with technology)
- Use information from a display to solve a problem and analyze the validity of statistical conclusions found in the media
- Use and justify range and measures of central tendency to determine the best representation of the data for a practical situation
- Use a line of best fit to describe trends and make predictions about data
- Identify and/or show the meaning of a best fit line
- Determine and compare the experimental and theoretical probability of independent and dependent events
- Explain in words and identify the difference between experimental and theoretical probability of independent and dependent events
- Analyze data to make predictions about the probability of independent and dependent events as a basis for solving real-world problems
- Design, conduct, analyze, and communicate the results of a multi-stage probability experiment
|
| Functions & Relationships
|
- Describe and extend patterns (families of functions: linear, quadratic, absolute value, square root) up to the nth term, represented in tables, equations, graphs, and real-world situations
- Generalize equations and inequalities (linear, quadratic, absolute value, square root) using a table of ordered pairs or a graph
- Describe in words how a change in one variable or constant in an equation affects the outcome of the equation
- Use a calculator as a tool when describing, extending, representing, or graphing patterns, linear equations, and quadratic equations
- Model (graphically and algebraically) and solve problems (including real-world applications) using systems of linear equations or inequalities
- Solve and identify solutions to multi-step linear equations of the form ax ± b = cx ± d, where a ,b, c, are rational numbers and a ≠ 0, c ≠ 0
- Solve and identify solutions to literal equations and formulas for a given variable involving multi-steps
|
| Geometry
|
- Determine the slope of a line using equations, formulas, tables, and graphs on a coordinate plane
- Draw, measure, and construct geometric models or plane figures containing parallel and/or perpendicular lines
- Graph a line segment on a coordinate grid and identify its length and midpoint by using formulas
|
| Problem Solving
|
- Select, modify, and apply a variety of problem-solving strategies and verify the results
- Apply multi-step integrated mathematical problem-solving strategies
- Evaluate, interpret, and justify solutions to problems by using an alternative strategy
- Represent mathematical problems numerically, graphically, and algebraically, communicate math ideas in writing ; and use appropriate vocabulary, symbols, or technology to explain, justify, and defend strategies and solutions
- Follow and evaluate an argument, judge its validity using inductive or deductive reasoning and logic; or make and test conjectures
- Explain why one strategy is more appropriate than another and determine why the estimated result is greater or less than the exact answer
- Use methods of informal proof including direct, indirect, and counterexamples to validate conjectures
- Apply mathematics to real-world contexts such as science, humanities, peers, community, careers, national issues, and global issues
|
Grade(s): 9-11
Length: Two semesters
Prerequisites:
| Numbers and Operations
|
- Converts between a rational number in scientific notation and standard form
- Equate different equivalent representatives of the same exponential expression
- Use models, explanations, number lines and real-life situations to describe and illustrate the effects of arithmetic operations on real numbers
- Use models, explanations, number lines and real-life situations to describe and illustrate the use of inverse operations (squaring/square root)
- Identify and apply commutative, identity, associative, inverse, and distributive properties to real numbers and variables
- Judge whether a strategy will result in an answer greater or less than the exact answer
- Add, subtract, multiply, and divide rational numbers including integers with whole number exponents
- Multiply and divide numbers in scientific notation
- Apply basic operations with real numbers using powers
|
| Measurement
|
- Estimate or convert measurements between the English and metric systems in real-world applications, given a conversion factor
- Apply indirect methods to find missing dimensions in real-world applications
|
| Statistics & Probability
|
- Design, collect, organize, display, or explain the classification of data in real-world problems, using information from tables and graphs that display two sets of data( or with technology)
- Use information from a variety of displays and analyze the validity of statistical conclusions found in the media
- Use range and measures of central tendency to determine the best representation of the data for a practical situation
- Use a best fit line to describe trends and make predications about data
- Identify and/or show the meaning of a best fit line
- Determine or compare the experimental and/or theoretical probability of independent or dependent events
- Design, conduct, analyze, and communicate the results of a multi-stage probability experiment
- Make predictions about the probability of independent or dependent events and use the information to solve problems
|
| Functions & Relationships
|
- Determine rate by using ratio and proportion
- Generalize relationships (linear) using a table of ordered pairs, a graph, and an equation
- Use a calculator as a tool when describing, extending, representing, and graphing patterns
- Solve or identify solutions to multi-step linear equations of the form ax ± b = cx ± d, where a ,b, c, are rational numbers and a ≠ 0, c ≠ 0
- Solve and identify solutions to literal equations or formulas for a variable involving multi-steps
- Introduce linear functions represented in tables, equations, graphs, and in real-world situations
- Introduce the movement between words, graphs, tables, and equations for linear relationships
|
| Geometry
|
- Determine the area and perimeter of 2-dimensional figures
- Graph one-dimensional solutions to linear equations and inequalities
|
| Problem Solving
|
- Select, modify, and apply a variety of problem-solving strategies and verify the results
- Evaluate, interpret, and justify solutions to problems by using an alternative strategy
- Represent mathematical problems numerically, graphically, and algebraically, translate among these alternative representations; and use appropriate vocabulary, symbols, or technology to explain, justify, and defend strategies and solutions
- Follow and evaluate an argument, judge its validity using inductive or deductive reasoning and logic; and make and test conjectures
- Describe in words how a change in one variable in a formula affects the remaining variables
- Describe in words how a change in one variable or constant in an equation affects the outcome of the equation
|
Grade(s): 10-12
Length: Two semesters
Prerequisites: Algebra A
| Numbers and Operations
|
- Identify the subsets of real numbers (natural, whole, integers, rational, irrational)
- Simplify expressions with positive and negative exponents
- Describe and illustrate the effects of arithmetic operations on real numbers
- Describe and illustrate the use of inverse operations (cubing/cube root)
- Identify and apply commutative, identity, associative, inverse, and distributive properties to real numbers and variables
- Identify and write the prime factorization of a variable expression using exponents
- Apply basic operations with real numbers using powers
- Solve and identify solutions to literal equations or formulas for a given variable involving multi-steps
|
| Measurement
|
- Use dimensional analysis to convert from one unit to another within and between English and metric systems in real-world applications
- Apply indirect methods, such as the Pythagorean Theorem to find missing dimensions in real-world applications
|
| Statistics & Probability
|
- Design, collect, organize, display, and explain the classification of data in real-world problems, using information from tables and graphs that display two or more sets of data( or with technology)
- Use information from a display to solve a problem and analyze the validity of statistical conclusions found in the media
- Use and justify range and measures of central tendency to determine the best representation of the data for a practical situation
- Use a line of best fit to describe trends and make predictions about data
- Explain in words or identify the difference between experimental and theoretical probability of independent or dependent events
- Analyze data to make predictions about the probability of independent or dependent events as a basis for solving real-world problems
- Design, conduct, analyze, and communicate the results of a multi-stage probability experiment
|
| Functions & Relationships
|
- Generalize equations and inequalities (linear, quadratic, absolute value) using a table of ordered pairs and a graph
- Use a calculator as a tool when describing, extending, representing, or graphing patterns, linear equations, or quadratic equations
- Model (graphically and algebraically) and solve problems (including real-world applications) using systems of linear equations and inequalities
- Select and use the quadratic formula or factoring to solve quadratic equations
- Solve problems involving percent increase or decrease
- Introduce and move between quadratic and absolute value functions as a table, graph and equation
|
| Geometry
|
- Determine the slope of a line using equations, formulas, tables, and graphs on a coordinate plane
- Draw, measure, and construct geometric models or plane figures containing parallel and/or perpendicular lines
- Graph a line segment on a coordinate grid and identify its length and midpoint by using formulas
|
| Problem Solving
|
- Apply multi-step integrated mathematical problem-solving strategies
- Verify the answer by using an alternative strategy
- Represent mathematical problems numerically, graphically, and algebraically, communicate math ideas in writing ; and use appropriate vocabulary, symbols, or technology to explain, justify, and defend strategies and solutions
- Use methods of informal proof including direct, indirect, and counterexamples to validate conjectures
- Explain why one strategy is more appropriate than another and determine why the estimated result is greater or less than the exact answer
|
Grade(s): 9th
Length: Two semesters
Prerequisites: Teacher recommendation
| Numbers and Operations
|
- Identify, describe, and illustrate equivalent representations of rational numbers (fractions, decimals, and percents including integers)
- Express products of numbers using exponents of rational numbers (fractions, decimals, and percents including integers)
- Apply the rules for order of operations to rational numbers
- Apply the rules for order of operations to real numbers and variables
- Identify and write the prime factorization of a number using exponents
- Use the distributive property with real numbers and variables
- Judge whether the strategy will result in an answer greater or less than the exact answer
- Add, subtract, multiply, and divide integers or positive rational numbers
- Use percents and percentages
- Convert between equivalent fractions, decimals, or percents
- Determine rate by using ratios and proportions
|
| Measurement
|
- Convert measurements within the same system (English or metric)
- Estimate or convert measurements between the English and metric systems in real-world applications, given a conversion factor
- Apply indirect methods, such as, Pythagorean Theorem to find missing dimensions in real-world applications
- Model the conversion within the same system
- Measure accurately using English and metric systems
|
| Statistics & Probability
|
- Design, collect, organize, display, and explain the classification of data in real-world problems using histograms, scatter plots, and box and whisker plots with appropriate scale (or with technology)
- Design, collect, organize, display, and explain the classification of data in real-world problems using information from tables or graphs that display two sets of data (or with technology)
- Use information from a variety of displays or analyze the validity of statistical conclusions found in the media
- Determine and justify a choice of range, mean, median, or mode as the best representation of data for a practical situation
- Identify and show the meaning of a best fit line
- Determine and compare the experimental and theoretical probability of simple events
- Use a systematic approach to finding sample spaces or to make predictions about the probability of independent events and use the information to solve real-world problems
- Design and conduct a simulation to study a problem and communicate the results
|
| Functions & Relationships
|
- Describe and extend patterns (linear) up to the nth term represented in tables, sequences, graphs, or in problem situations
- Generalize relationships (linear) using a table, ordered pairs, a graph, or an equation
- Describe in words how a change in one variable in a formula affects the remaining variables (how changing the length affects the area of quadrilaterals and volume of a rectangular prism)
- Use a calculator as a tool when describing, extending, and representing patterns
- Translate a written phrase to an algebraic expression
- Solve or identify solutions to two-step linear equations of the form ax ± b = c, where a ,b, and c, are rational numbers and a ≠ 0; translating a story problem into an equation of similar form; or translating a story problem into an equation of similar form and solving it
|
| Geometry
|
- Use the attributes and properties or regular polygons to sketch regular or irregular polygons
- Use attributes and properties of solid figures (vertices, length and alignment of edges, shape and number of bases) to identify and describe cylinders and cones
- Use 2-dimensional nets to create 3-dimensional objects (prisms and cylinders)
- Identify, analyze, compare, and use properties of angles (including supplementary or complementary) or circles (degrees in a circle)
- Use proportionality to solve real-world problems involving similar shapes
- Determine the circumference and area of a circle
- Draw, measure, and construct geometric figures(polygons, perpendicular bisectors, or perpendicular or parallel lines)
|
| Problem Solving
|
- Select, modify, and apply a variety of problem-solving strategies ( charts, graphing, inductive and deductive reasoning, Venn diagram, and making a simpler problem) and verify the results
- Evaluate, interpret, and justify solutions to problems
- Represent mathematical problems numerically, graphically, and symbolically, translating among these alternative representations; and use appropriate vocabulary, symbols and technology to explain, justify, and defend strategies and solutions
- Generalize from patterns of observations (inductive reasoning) about mathematical problems and testing using a logical verification (deductive reasoning); and justify and defend the validity of mathematical strategies and solutions using examples and counterexamples
- Use real-world contexts such as science, humanities, peers, community, and careers
|
Grade(s): 10-12
Length: Two semesters
Prerequisites: Advanced Algebra (or equivalent)
| Numbers and Operations
|
- Identify numbers as complex, real, irrational, rational, integers, whole, or natural
- Simplify expressions with complex numbers, positive and negative exponents, and rational exponents
- Write expressions in simplest radical form
- Describe and illustrate the affects of arithmetic operations on complex numbers
- Describe and illustrate the use of inverse operations
- Identify and apply commutative, associative, distributive, identity and inverse properties to complex numbers and variables
- Apply basic operation on matrices
|
| Trigonometry
|
- Use graphs of the unit circle and circular functions to explain, illustrate and calculate trigonometric values
- Express angle displacement in revolutions, degrees and radians
- Use graphs of circular functions to explain, illustrate, and calculate trigonometric solutions
- Apply right triangle trigonometry to solve right triangles
- Apply Law of Sines and Law of Cosines to solve oblique triangles
- Verify equivalent trigonometric expressions using trigonometric identities
- Find exact trigonometric values using trigonometric identities (sum, difference, half angles and double angles)
- Apply trigonometric identities to simplify and solve trigonometric equations
- Apply trigonometric relationships to solve vector problems
- Apply properties of the unit circle to solve trigonometric relationships and equations
|
| Statistics & Probability
|
- Collect, design, organize, display, and explain data in real-world contexts: science, humanities, among peers, community, and careers
- Use information from tables, graphs, and displays with multiple sets of data to solve problems
|
| Functions & Relationships
|
- Generalize equations and inequalities involving polynomial, rational, trigonometric, exponential and logarithmic, square root, absolute value, step, radical and piecewise functions
- Use technology including graphing calculators and computers to describe, extend, represent, and graph patterns of polynomial, rational, trigonometric, logarithmic, and exponential equations
- Identify, graph, model and find equations for the conic sections
- Identify and graph points in both rectangular and polar coordinate systems.
- Describe the characteristics of a graph of a function:
intercepts
maximums and minimums
asymptotes using limits
symmetry
end behavior
continuity
domain and range
|
| Problem Solving
|
- Explain why one strategy is more appropriate than another
- Find alternative methods for solving problems
- Communicate solutions and strategies using appropriate vocabulary and mathematical units
- Use methods of proof to validate conjectures, including direct, indirect and counterexamples
- Apply multi-step integrated mathematical problem solving strategies
- Verify solutions using alternative strategies
- Represents problems in a mathematical format using numbers, graphs, tables, illustrations, and symbols
- Use appropriate technology to analyze, solve, justify, and explain strategies and solutions
|
Grade(s): 11-12
Length: Two semesters
Prerequisites: 2 years of high school math
| Numbers and Operations
|
- Read, write model and order real numbers, explaining percents.
- Translate between equivalent representations of the same number. Select a representation that is appropriate for the situation.
- Describe and model the relationship of fractions to decimals, percents, ratios, and proportions.
- Use estimation to solve problems and to check the accuracy of solutions; state whether the estimation is greater or less than the exact answer.
- Apply basic operations efficiently and accurately, using estimation to check the reasonableness of results.
- Add, subtract, multiply and divide rational numbers in various forms including fractions, decimals, and percents.
- Solve problems using ratio and proportion.
- Select, convert, and apply an equivalent representation of a number for a specified situation.
|
| Measurement
|
- Estimate and convert measurements within systems.
- Apply various measurement systems to describe situations and solve problems.
- Apply information about elapsed time to solve problems.
|
| Statistics & Probability
|
- Determine and justify a choice of mean, median, or mode as the best representations of data for a practical situation.
|
| Geometry
|
- Estimate and determine volume and surface areas of solid figures using formulas.
|
| Problem Solving
|
- Analyze and summarize a problem using the relationship between the known facts and unknown information.
- Recognize and formulate mathematical problems from within and outside the field of mathematics.
- Apply multi-step, integrated, mathematical problem-solving strategies, persisting until a solution is found or it is clear that no solution exists.
- Evaluate, interpret, and justify solutions to problems.
|
| Communication
|
- Represent a problem numerically, graphically, and symbolically; translate among these alternate representations.
- Use appropriate vocabulary, symbols, and technology to explain, justify, and defend mathematical solutions.
|
| Connections
|
- Apply mathematical skills and processes to global issues.
- Describe how mathematics can be used in knowing how to prepare for careers.
|
Philosophy:
Students do best when they have an understanding of the conceptual underpinnings of Calculus. Rather than making the course a long list of skills that students have to memorize, the “why” behind the major ideas must be stressed. As we develop the major concepts, we will explain how the mechanics go along with the topics and apply them to real life situations.
Students enrolled in this class must have a graphing calculator that meets the AP College Board calculator requirements. The calculator will be required on some assessments and used as a tool to help students develop an intuitive feel for the concepts.
Unit 1: Precalculus Review
In order to be successful in Calculus, students need a firm grasp on the prerequisite topic. Therefore to assist the students in this requirement 2 -3 weeks will be spent reviewing the following topics
- Lines
- Slope as a rate of change
- Parallel and perpendicular lines
- Equations of lines
- B. Functions and graphs
- Functions
- Domain and range
- Families of functions
- Piecewise functions
- Composition of functions
- C. Exponential Growth and Logarithmic functions
- Exponential growth and decay
- Inverse functions
- Logarithmic functions
- Properties of logarithms
- D. Trigonometric Functions
- Graphs of basic trigonometric functions
- Domain and range
- Transformations
- Inverse trigonometric functions
- Applications
Calculus is made up of 4 main concepts: Limits, Derivatives, Indefinite Integrals and Definite Integrals. The 4 concepts will be explored numerically, graphically, algebraically and verbally. The calculator will have an integral part in the study of these concepts.
Unit 2: Limits and Continuity (3 weeks)
- Rates of change and Limits
- Average and instantaneous speed
- Definition of limit
- Properties of limit
- One-sided and two-sided
- Squeeze theore
- Limits involving infinity
- Asymptotic and end behavior
- Visualizing limits
- Continuity
- Continuity at a point
- Continuous functions
- Discontinuous functions
- Removable discontinuity
- Jump discontinuity
- Infinite discontinuity
- Intermediate Value Theorem
- Rates of change and Tangent lines
- Average rate of change
- Tangent to a curve
- Slope of a curve
- Normal to a curve
Unit 3: Derivative (5 weeks)
- Derivative of a function
- Definition of a derivative
- Notation
- Relationship between the graphs of
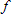 and
and 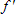
- Graphing the derivative from data
- B. Differentiability
- Local linearity
- Numeric derivatives using the calculator
- Differentiability and continuity
- Intermediate Value Theorem for derivatives
- Rules for differentiation
- Applications to velocity and acceleration
- Derivatives of trigonometric functions
- Chain rule
- Implicit differentiation
- Derivatives of inverse trigonometric functions
- Derivatives of logarithmic and exponential functions
Unit 4: Applications of the Derivative (4 weeks)
- Extreme values
- Local (relative) extrema
- Global (absolute) extrema
- Applying the derivative
- Mean Value Theorem
- Physical interpretatio
- Rolle’s Theorem
- Increasing and decreasing function
- Analysis of graphs using the first and second derivatives
- Critical values
- First derivative test for extrema
- Concavity and points of inflection
- Second derivative test for extrema
- Modeling and optimization problems
- Linearization models
- Related rates
Unit 5: The Definite Integral (3 weeks)
- Approximation of Area
- Riemann sums
- Trapezoidal rule
- Geometrically
- Definite integrals
- Terminology and notation
- Definite integral and area
- Integrals on the calculator
- Definite integrals and antiderivatives
- Properties of definite integrals
- Average value of a function
- Mean Value Theorem
- Connecting differential and integral calculus
- The Fundamental Theroem of Calculus
- Fundamental Theorem Part 1
- Graphing the function
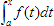
- Fundamental Theorem Part 2
- Analyzing antiderivatives graphically
Unit 6: Differential Equations and Mathematical Modeling (3-4 weeks)
- Slope fields
- Differential Equations
- Antiderivatives by substitution
- Indefinite integrals
- Substitution in indefinite integrals
- Substitution in definite integrals
- Exponential growth and decay
- Separable differential equations
- Continuously compounded interest
- Modeling growth with other bases
Unit 7: Applications of Definite Integrals (3 weeks)
- Integral as net change
- Linear motion
- General strategy
- Consumption over time
- Net change from data
- Work
- Areas in the plane
- Volumes
- Volumes of solids with known cross sections
- Volumes of solids of revolution (Disk and Shell methods)
Unit 8: Review for AP Exam (4 -5weeks)
Finney, Ross L., Franklin D. Demana, Bert Waits, and Daniel Kennedy.
Calculus – Graphical, Numerical, Algebraic. 3rd ed. Boston Massachusetts: Pearson Prentice Hall, 2007.
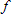 and
and